# 이진탐색트리 (Binary Search Tree)
# 이진탐색트리의 목적은?
이진탐색 + 연결리스트
이진탐색 : 탐색에 소요되는 시간복잡도는 O(logN), but 삽입,삭제가 불가능
연결리스트 : 삽입, 삭제의 시간복잡도는 O(1), but 탐색하는 시간복잡도가 O(N)
이 두가지를 합하여 장점을 모두 얻는 것이 '이진탐색트리'
즉, 효율적인 탐색 능력을 가지고, 자료의 삽입 삭제도 가능하게 만들자
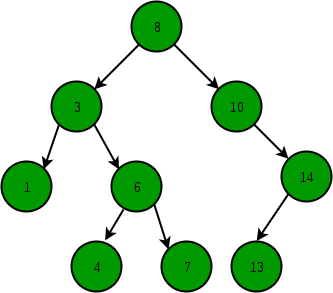
# 특징
- 각 노드의 자식이 2개 이하
- 각 노드의 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 큼
- 중복된 노드가 없어야 함
중복이 없어야 하는 이유는?
검색 목적 자료구조인데, 굳이 중복이 많은 경우에 트리를 사용하여 검색 속도를 느리게 할 필요가 없음. (트리에 삽입하는 것보다, 노드에 count 값을 가지게 하여 처리하는 것이 훨씬 효율적)
이진탐색트리의 순회는 '중위순회(inorder)' 방식 (왼쪽 - 루트 - 오른쪽)
중위 순회로 정렬된 순서를 읽을 수 있음
# BST 핵심연산
- 검색
- 삽입
- 삭제
- 트리 생성
- 트리 삭제
# 시간 복잡도
- 균등 트리 : 노드 개수가 N개일 때 O(logN)
- 편향 트리 : 노드 개수가 N개일 때 O(N)
삽입, 검색, 삭제 시간복잡도는 트리의 Depth에 비례
# 삭제의 3가지 Case
자식이 없는 leaf 노드일 때 → 그냥 삭제
자식이 1개인 노드일 때 → 지워진 노드에 자식을 올리기
자식이 2개인 노드일 때 → 오른쪽 자식 노드에서 가장 작은 값 or 왼쪽 자식 노드에서 가장 큰 값 올리기
편향된 트리(정렬된 상태 값을 트리로 만들면 한쪽으로만 뻗음)는 시간복잡도가 O(N)이므로 트리를 사용할 이유가 사라짐 → 이를 바로 잡도록 도와주는 개선된 트리가 AVL Tree, RedBlack Tree
← - 트리(Tree) - 해시(Hash) →